What is a Fraction?
A fraction is a value in math that represents equal parts of a whole number. You can take a number like 1 and divide it into 6 equal parts. Think about a pie for this one. You have one pie and then you cut it into six equal pieces. Each of those pieces represents one sixth of the pie. When you write that one piece as a fraction, you will write 1/6. If you write the whole pie as a fraction, you write 6/6, since it has all six pieces. The top number, the numerator, represents how many you have. The bottom number, the denominator, represents the number of possible equal parts. When the number of pieces you have is the same as the number of possible pieces (6/6) you have a whole number (1). Problem:
Problem:Let's say you have a pie that was sliced into 8 pieces. There are only 3 pieces of pie left in the tin. What is the fraction that represents the number of pieces in the tin?
Answer:
3/8 (three pieces of a possible eight). That means three eighths of the pie is left.
Problem:
I have a bunch of bananas. There were originally 9 bananas but I only have 2 left. What is the fraction that represents how many bananas I have left?
Answer:
2/9 (two bananas of a possible nine). That means only two ninths of my bananas are left.
Basic Parts of a Fraction
The two big terms in fractions are numerators and denominators. A fraction has a top number and a bottom number. Numerators are on the top and denominators are on the bottom. It is that simple.1/9: Numerator =1 and Denominator = 9
10/97: Numerator = 10 and Denominator = 97
11/19: Numerator = 11 and Denominator = 19
The structure matters when you start to think about fractions as division problems. The numerator is the first number in a division problem (dividend). The denominator is the second number in a division problem (divisor).
1/9 = 1 ÷ 9: Dividend = 1 and Divisor= 9
10/97 = 10 ÷ 97: Dividend = 10 and Divisor = 97
11/19 = 11 ÷ 19: Dividend =11 and Divisor = 19
There is one major rule you must remember about fractions. The denominator (bottom value) can NEVER be 0. You cannot divide numbers by zero in any of our problems. You can divide things by one. That's easy. Any number divided by one is itself (15/1 = 15÷1 = 15). The denominator can never be zero.
Different Ways of Writing Fractions
Let's look at equivalent fractions first. You might have the fraction one-half (1/2). An equivalent fraction is any fraction that equals 1/2 when it is reduced.Here's another way to think about it. When you divide 1 by 2 (1÷2), your answer is 0.5. Any division problem that has the same answer can be written as an equivalent fraction. For example, 284÷568=0.5. We can rewrite the division problem as 284/568. That is an equivalent fraction to 1/2 because they have the same quotient.
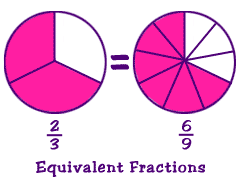 You can also create an equivalent fraction when you multiply by 1 in fraction form. Any number multiplied by 1 is equal to the original number. When you learn more about math, you will learn the ability to multiply by 1 is called the identity property. You can guess that 1/1 is one, but 13/13 and 27/27 are also equal to one. They are all equivalent fractions. If you use a fraction that is equivalent to one, you can solve a bunch of problems. You wind up multiplying the numerator and denominator by the same number to make new equivalent fractions.
You can also create an equivalent fraction when you multiply by 1 in fraction form. Any number multiplied by 1 is equal to the original number. When you learn more about math, you will learn the ability to multiply by 1 is called the identity property. You can guess that 1/1 is one, but 13/13 and 27/27 are also equal to one. They are all equivalent fractions. If you use a fraction that is equivalent to one, you can solve a bunch of problems. You wind up multiplying the numerator and denominator by the same number to make new equivalent fractions.
Example: 5/6
• Remember that anything multiplied by 1 is the same as the original number.
• That tells us that 5/6 * 1 = 5/6
• Instead of 1, let's substitute the equivalent fraction 5/5. The new version changes from 5/6 * 1 to 5/6 * 5/5.
• Multiply the top and bottom by 5. 5x5 on top and 6x5 on the bottom.
• You get the fraction 25/30.
• 25/30 is equivalent to 5/6.
• All together... 5/6 = 5/6 * 1 = 5/6 * 5/5 = 25/30
Think about that last idea for a second. All we did was multiply by different versions of 1. The numbers changed, but the values always stayed the same. On your own, think about one fraction that is equivalent to 1/3. You might have 2/6, 3/9, 4/12, 5/15. The list goes on forever.
You'll also hear about like fractions and unlike fractions. Like fractions have the same denominators. They have common denominators. An example might be 2/15, 4/15, 8/15, and 14/15. Those are all like fractions. You will need like fractions when you add and subtract fractions. Unlike fractions have different denominators. 7/15 and 8/19 are unlike. You'll have to find a way to make all of your fractions "like fractions" before you start to add and subtract. We'll use easier examples when you get there.
Reciprocals are fractions that have been flipped. If you have the fraction 8/13, its reciprocal is 13/8. If you want to get technical, when you multiply reciprocal fractions, the answer will always be 1. We'll look at that fact when you divide fractions. You'll use reciprocals and flipping on the second term of those division problems.
Fractions and Division
A fraction is a division problem at its heart. 1/2 is the same thing as 1÷2. Many problems will ask you to turn division problems into fractions. A division problem such as 17÷8 is equal to 2 with a remainder of one. When it comes time to write the fraction, you will have a mixed number. The answer 2r1 converts into 2 1/8. That remainder of one is basically the left over bit of division. Like this...Problem:
What is 23 ÷ 5 as a mixed number?
Answer:
• When you do the division, you get 4 with a remainder of 3.
|
4 r 3 5 ) 23 - 20 3 |
• The whole number is 4 and the remainder is 3. You were originally dividing by 5.
• The format of the mixed number is the whole number and a fraction. The remainder is the numerator and the divisor is the denominator (remainder/divisor).
• 4 3/5 is your final answer.
You can also think of the final answer this way...
23 ÷ 5 = 23/5 = 20/5 + 3/5 = 4 + 3/5 = 4 3/5

- Overview
- Number Types
- Factors
- Fractions
- Structure
- Reducing
- More or Less
- Mixed Numbers
- Mixed Numbers 2
- Addition
- Subtraction 1
- Subtraction 2
- Multiplication
- Division
- Word Problems
- Real World
- Decimals
- Percentages
- Estimation
- Ratios
- Money
- Activities
- More Maths Topics

Useful Reference Materials
Wikipedia:https://en.wikipedia.org/wiki/Fraction_%28mathematics%29
Encyclopædia Britannica:
http://www.britannica.com/topic/fraction
University of Delaware:
https://sites.google.com/a/udel.edu/fractions/